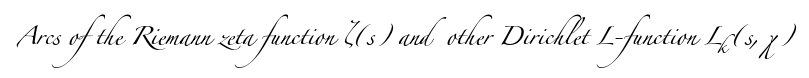A recent birthday present (my 36th) was Elias Wegert's Visual complex functions. On the sides of the pages are strips -- excerpts from the critical strip of the Riemann zeta function with nontrivial roots. He wrote a paper about the stochastic period of 2$\pi$, which is easily observable in the below image as the yellow diagonals:

He's got the images of the functions up on a functions gallery on the website associated with the book. I thought I couldn't see what was going on so I used the gimp to prune the white regions from the images and to glue the remainders together. So, this led to a mathoverflow question after I asked Matt McIrvin to take a Fourier transform -- which he did with a set discretely supported on the roots of the Riemann zeta function, and a post on the n-category cafe concerning Freeman Dyson's speculation that the roots might form a quasicrystal. There are some obvious questions:

• What about other L-functions? The best way of performing such calculations is to use sage and its implementation of the Dokhitser L functions calculator.
• What is the local phase at each root (how much is each root rotated?) -- and this lives on U(1).